(School of Mathematics, Birmingham). Received on 8/2/2023.
In this note we will introduce the concept of character variety in the simple example of a torus with one disk removed. We will show how this is a surface in C^{3} defined by a cubic polynomial, called the Markov cubic. We will show the relation between the Markov cubic, singularity theory, Painlevé differential equations, and introduce a cluster algebra structure on it which is related to Markov numbers. We will discuss quantisation of the Markov cubic in the context of a wider class of surfaces and relate it to Sklyanin algebra.
Main motivation
“Symmetry, as wide or narrow as you may define its meaning, is one idea by which humans through the ages have tried to comprehend and create order, beauty and perfection” (Hermann Weyl). As mathematicians, we chase symmetry. The most profound and far reaching idea in physics is Emmy Noether theorem: the symmetries of a system imply the existence of conserved quantities along its evolution.
One of the most puzzling symmetries discovered nowadays is mirror symmetry (MS). In string theory, particles are replaced by strings and six extra small dimensions are needed to describe the universe. These are wrapped up in Calabi-Yau (CY) varieties that occur in pairs: CY in the same pair produce equivalent physical theories. Following Noether’s idea, one way to comprehend MS is to study its fixed points, namely self mirrors. In this note I will discuss some examples of self mirrors which appear in several different contexts in mathematics.
Toy introduction to MS: Quantum mechanics analogy
By the Stone–von Neumann theorem, these two pictures are equivalent (just a basis change in the Hilbert space).
Mirror symmetry
Similarly to the case of quantum mechanics, in MS we have two different sides: an A-side and a B-side.
Mirror pairs of CY varieties (compact Kähler manifolds with vanishing first Chern class and Ricci flat metric) are of very different nature but the symplectic geometry of the A-side is reflected in the algebraic geometry of its mirror:
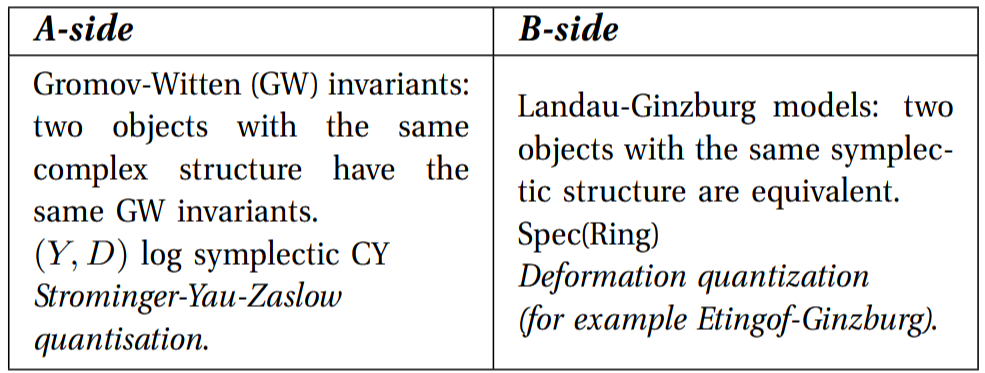
The physical theories produced by the two sides are equivalent.
The aim of this note is to present a class of examples (affine del Pezzo varieties) that are self mirrors (can be on both sides). These examples are relevant in several branches of mathematics:
- Number theory
- Singularity theory
- Orthogonal polynomials
- Moduli spaces
- Painlevé equations
- Cluster algebras
The Markov cubic
Starting from (1, 1, 1), all Markov triples are produced by permutations and Vieta jumping equivalent to the following three operations called “mutations”:
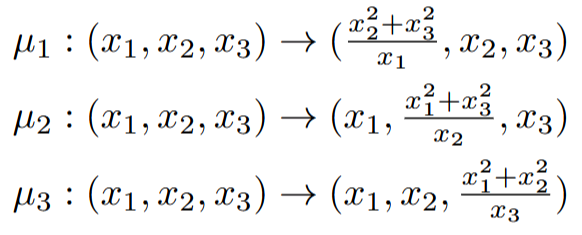
Examples:
Note that despite dividing by an integer at each step, the result is not a rational number, but an integer again. This is a consequence of the so-called Laurent phenomenon in cluster algebra.
Cluster algebras
This is a class of commutative rings introduced by Fomin-Zelevinsky in 2002. They are integral domains with some sets of size n called clusters. Given a cluster 
, all other clusters are generated by mutations of the form
where m_{1} and m_{2} are monomials in obeying some rules.
Theorem (Laurent phenomenon). Given any two clusters in a cluster algebra, and 
, then 
is a Laurent polynomial of , i = 1, . . . , n.
Example. The integers Z with the Markov triples form a cluster algebra, therefore any component of a Markov triple is a
Laurent polynomial of (1, 1, 1). The Markov cubic is related to the character variety of a torus with one boundary.
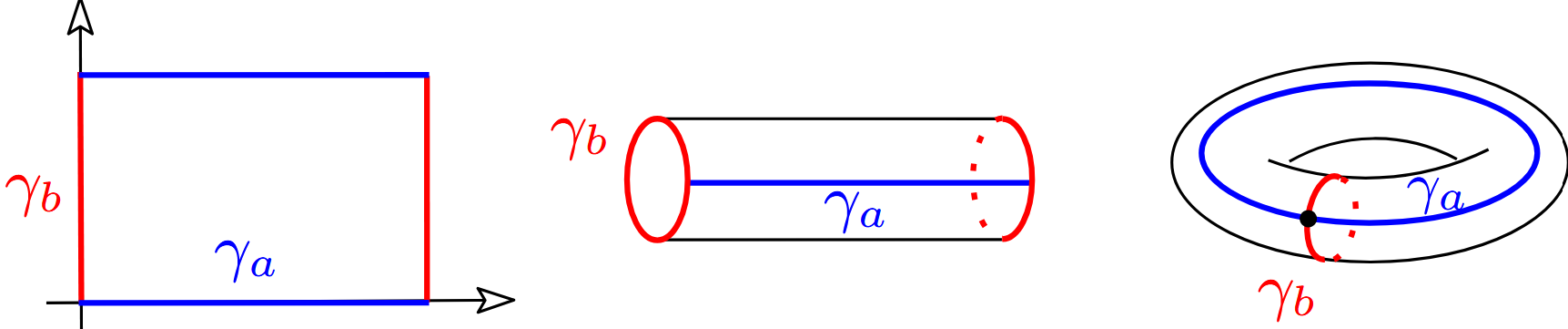
Standard torus 
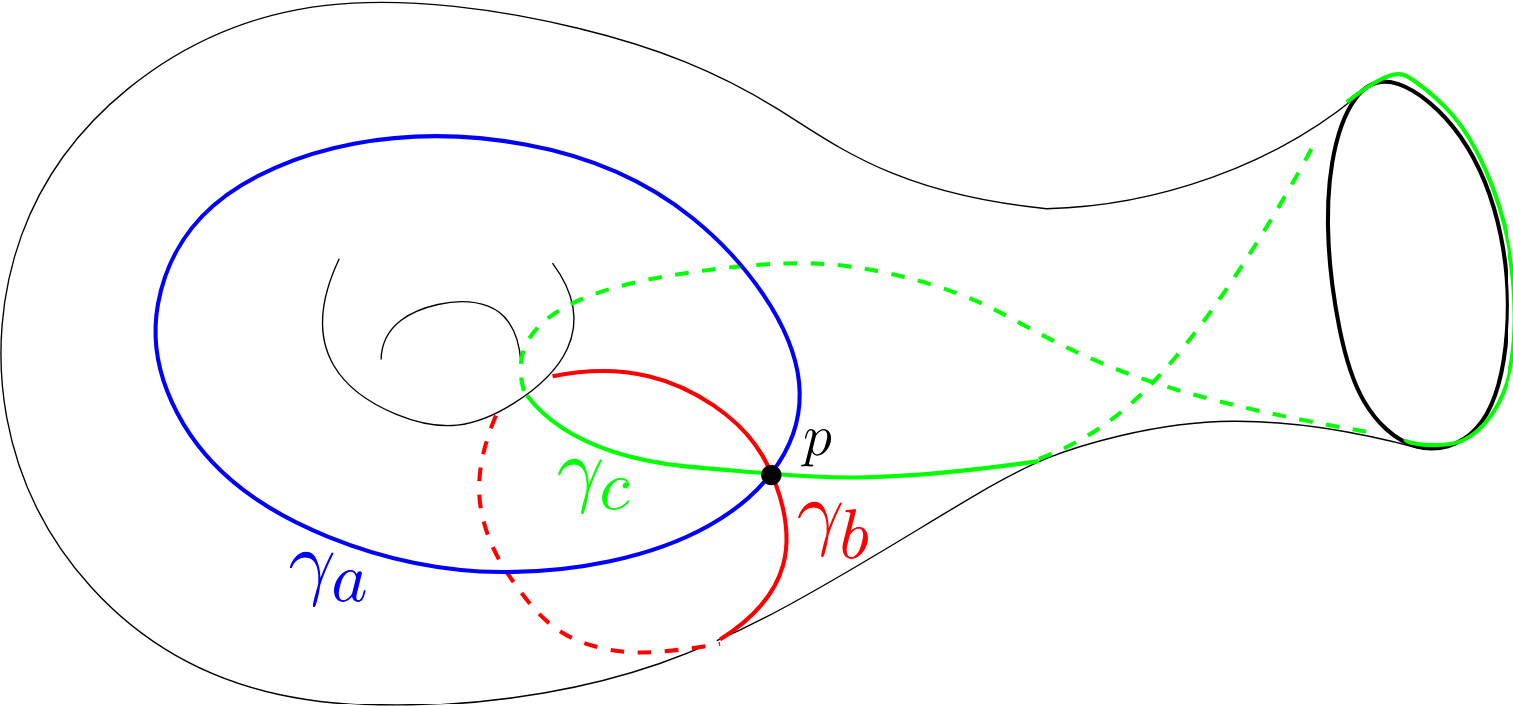
Torus with one boundary 
γ_{0} loop around the removed disk.
Its character variety is defined as 
. To write this as an affine surface, 
, M_{a}M_{b}M_{c} = M_{0} up to a global conjugation. Thus tr(M) are invariant and x_{i} = tr(M_{i}) for i = a, b, c satisfy a cubic equation:
This is equivalent to the Markov cubic up to a rescaling of x_{a}, x_{b}, x_{c}.
Character variety of the 4-holed sphere
By a quadratic transformation, the Markov cubic is related to the character variety of a sphere with 4 punctures. More generally, for the case of 4 holes, this is:
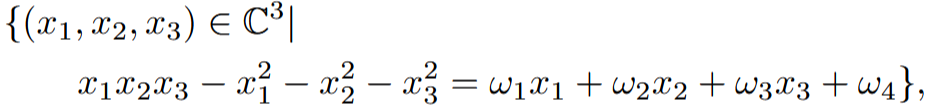
where ω_{1}, ω_{2}, ω_{3}, ω_{4} ∈ C are parameters.
- Monodromy manifold of the sixth Painlevé equation.
- Versal deformation of a du Val D4 singularity at (2, 2, 2).
- Most importantly, it is self mirror (see [1]).
I will show how to quantise a wide class of affine surfaces that contains this example as a sub-case.
Quantization of affine surfaces
We focus on a special class of affine surfaces of the form
where
with deg(ϕi) ⩽ 6. Examples:
- Affine del Pezzo surfaces: blowup of 9 − d points of P^{2}.
- Deformations of elliptic singularities (e.g. affine cone surfaces with elliptic singularity) [2] and Kleinian sigularities [3] (weighted projective del Pezzo with a nodal singularity).
Poisson structure. Given any φ ∈ C[x_{1}, x_{2}, x_{3}], we get a Poisson bracket on C[x_{1}, x_{2}, x_{3}], i.e. a bilinear map
that is skew-symmetric and satisfies the Leibniz rule and the Jacobi identity. This is defined in terms of the potential φ as:
Note that the potential φ not only defines the Poisson relations but is also central {φ, ·}. Therefore the Poisson structure descends to the ring of functions on the surface 
. In other words, 
is a Poisson algebra, so that the affine del Pezzo surface given by the zero set of φ,
Z(φ), is Spec(A_{φ}).
For our chosen φ we have
To quantize, we define a suitable Lie algebra isomorphism:
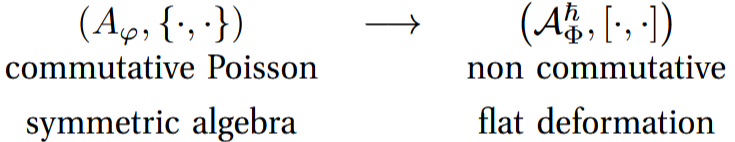
Example: For
we obtain the Askey-Wilson algebra [4]
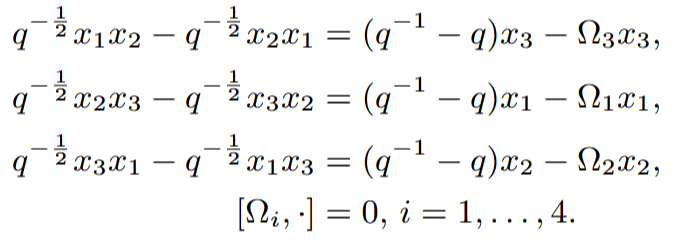
Semiclassical limit: 
gives the character variety of a sphere with four boundaries.
The Painlevé–Sklyanin algebra
Definition. For any choice of the scalars
such that α_{i} are not roots of unity, the generalised Sklyanin-Painlevé algebra is the non-commutative algebra with generators X_ {1}, X_{2}, X_{3} defined by the relations:
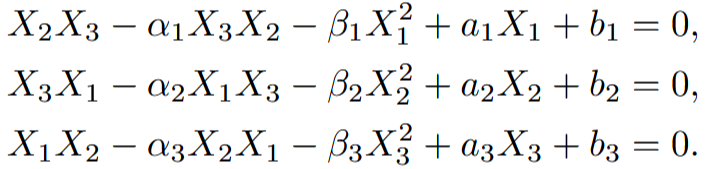
We fully characterise for which cases the generalised Sklyanin-Painlevé algebra is a Calabi Yau algebra has nice properties [5]:
Theorem. For specific choices of the parameters as follows:
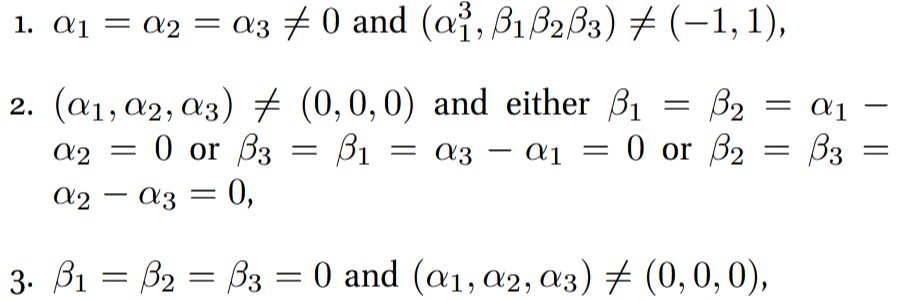
the generalised Sklyanin-Painlevé algebra is Calabi-Yau, has a Hilbert series with polynomial growth and is Koszul.
Note that for a_{i} = b_ {i} = 0, i = 1, 2, 3, the Sklyanin–Painlevé algebra restricts to the so called Artin–Schelter–Tate–Sklyanin algebra with three generators. For β_{1} = β_{2} = β_{3} = 0 and (α_{1}, α_{2}, α_{3}) ≠ (0, 0, 0) this algebra produces the monodromy manifolds of the Painlevé differential equation in the semiclassical limit.
References
[1] Mark Gross, Paul Hacking, Sean Keel, and Bernd Siebert, The mirror of the cubic surface (Hamid Abban, Gavin Brown, Alexander Kasprzyk, and Shigefumi Mori, eds.), LMS Lecture Notes Series, vol. 478, Cambridge University Press, 2022. In Recent Developments in Algebraic Geometry: To Miles Reid for his 70th Birthday, 150-182.
[2] P. Etingof and V. Ginzburg, Noncommutative del Pezzo surfaces and CalabiYau algebras, J. Eur. Math. Soc. 12 (2010), no. 6, 1371–1416.
[3] Pavel Etingof, Alexei Oblomkov, and Eric Rains, Generalized double affine Hecke algebras of rank 1 and quantized del Pezzo surfaces, Advances in Mathematics 212 (2007), no. 2, 749-796.
[4] Alexei Oblomkov, Double affine Hecke algebras of rank 1 and affine cubic surfaces, Int. Math. Res. Not. 18 (2004), 877-912.
[5] Leonid Chelhov, Marta Mazzocco, and Vladimir Rubtsov, Quantised Painlevé monodromy manifolds, Sklyanin and Calabi-Yau algebras, Advances in Mathematics 376 (2021), 2021.